Overview*
Most advanced classes in math physics focus on teaching students to do mathematical manipulations and methods appropriate for problems in physics. These problems are often couched in the language and context of physics, but often miss critical elements of the use of math in physics. In any science, mathematics provides a structure with well-specified rules and procedures. This works surprisingly1 well. Nonetheless, in realistic situations, the mathematics one uses depends on assumptions and approximations about the physical world -- it is a model. As such, its use and interpretation depends on skills other than mathematical methods. It requires an understanding of the modeling process and how to interpret the mathematical results obtained. We summarize this with the schematic figure below.
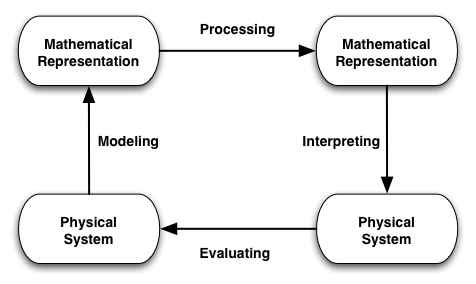
The materials accessible from this webpage -- readings and problems -- are intended as a supplement to a traditional math physics text that focus on aspects of math in physics beyond mathematical processing -- that involve modeling, interpreting, and evaluating as well.
Reading materials that review some basic mathematical issues and put them in a concrete and physical context.
A collection of ~50 problems (and solutions) that are appropriate for giving students the opportunity to work on more than just mathematical processing skills.
Papers discussing the use of mathematical modeling in science and research papers on student use of and difficulty with mathematical modeling in advanced physics classes.
*The development of these materials were supported in part by NSF Grant 05-24987, "Learning the language of science: Advanced math for concrete thinkers," E.F. Redish, P. I.
1 E. Wigner, "The Unreasonable Effectiveness of Mathematics in the Natural Sciences," in Communications in Pure and Applied Mathematics, vol. 13, No. I (February 1960).
Comments (0)
You don't have permission to comment on this page.